中学受験 · 2023/01/05
6の倍数は3の倍数で偶数のもの (6=2×3) 3の倍数は各位の数字の和が3で割り切れるもの 6の倍数は偶数でないといけないので □4□の 一の位は0、2、4、6、8の5通り 5通りのそれぞれに対し 百の位は3通りずつ ※ (1、4、7) (2、5、8) (3、6、9) のどれか 5×3=15(通り)
中学受験 · 2023/01/04
「ある数」の約数を探すには、かけ合わせて「ある数」になるペアの数字を見つける 12の約数は 1 2 3 12 6 4 30の約数は 1 2 3 5 30 15 10 6 2つ1組のペアだから 約数の個数は偶数であることが普通 奇数になるのはどういう場合か? 25の約数 1 5 25 5 36の約数 1 2 3 4 6 ...
中学受験 · 2022/12/25
7、14、21、28、35、42… これらは7ずつ増えていく7の倍数 7ずつ大きくなるので どのふたつを選んでも その差は7の倍数 例えば7と28の差は21 14と42の差は28 21、28、どちらも7の倍数
中学受験 · 2022/12/19
36の約数を書き出すと 1 2 3 4 6 36 18 12 9 6 約数の和は 1+2+3+4+6+9+12+18+36=91 このように足せばできるが 計算で求める方法も知っておきたい 36を素因数分解すると 36=2×2×3×3 =2²×3²
中学受験 · 2022/12/15
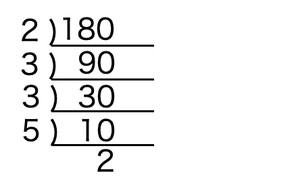
書き出して数えれば早いが ここでは計算で求める 12を素因数分解すると 12=2×2×3 出てくる素数は2と3 ↓ 2と3のグループに分ける 2のグループは1、2、4 1⋯2を0回かけたもの ※2をかけていない。2×0ではない) 2⋯2を1回かけたもの 4⋯2を2回かけたもの 3のグループは1、3 1⋯3を0回かけたもの 3⋯3を1回かけたもの...