180の約数は全部で何個ですか。

 

 

 

書き出して数えてもいいが、

ちょっとめんどうなので計算で求める

 

 

 

 

180を素因数分解すると

 

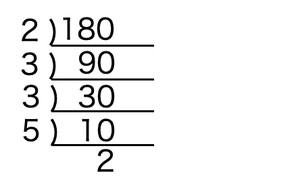
180＝２×２×３×３×５

 

 

出てくる素数は２と３と５

　↓

２と３と５のグループに分ける

 

 

 

２のグループは１、２、４

 

１⋯２を０回かけたもの

　※２をかけていない。２×０ではない）

２⋯２を１回かけたもの

４⋯２を２回かけたもの

 

 

 

３のグループは１、３、９

 

１⋯３を０回かけたもの

３⋯３を１回かけたもの

９⋯３を２回かけたもの

 

 

 

 

５のグループは１、５

 

１⋯５を０回かけたもの

５⋯５を１回かけたもの

 

 

グループの数字各１個ずつを３個かけ合わせたものが約数

 

  

 約数の個数は

３×３×２＝18（個）

 

 

 

 

（発展）

 

180＝２²×３²×５

 

２²の右上の小さい²は

２を何回かけ合わせたかを表すもので

「指数」と言う。〜乗（じょう）と読む

 

０乗（ゼロじょう）は１

２⁰＝１

３⁰＝１

５⁰＝１

N⁰＝１（Nは整数）

180＝２²×３²×５

５は５¹と表せるので

 

180＝２²×３²×５¹

 

 

 

２のグループは

２⁰＝１

２¹＝２

２²＝４

の３つ

 

３のグループは

３⁰＝１

３¹＝３

３²＝９

の３つ

 

５のグループは

５⁰＝１

５¹＝５

の２つ

 

180＝２²×３²×５¹

 

指数＋１がグループの個数

２²　２＋１＝３

３²　２＋１＝３ 

５¹　１＋１＝２ 

 

約数の個数は

各グループの個数をかけ合わせたもの

 

３×３×２＝18（個）