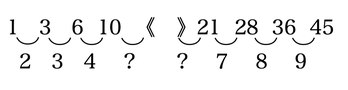中学受験 · 2022/11/27
1,3,5,7,9,11,‥‥は 奇数(2で割りきれない整数)の数列 整数を順番に並べると、 1、2、3、4、5、6、7、8⋯ のように、 奇数と偶数(2で割り切れる整数)が交互に出てくる これをふたつごとに区切っていくと、奇数と偶数のペアになる (1、2)(3、4)(5、6)(7、8)⋯ 1番目の奇数偶数(1、2) 2番目の奇数偶数(3、4)...
中学受験 · 2022/11/24
数字の間を調べると 3、5、7・・・15 奇数だと推測できる 数字間に 3、5、7、9、11、13、15 を当てはめると、 16+9=25 25+11=36 36+13=49 となるのでまちがいない 《 》にはいる数字は25、36 (別解) 数字の特徴は 1=1×1 4=2×2 9=3×3 16=4×4 ・ ・ 49=7×7 64=8×8 この間にあるのは 5×5=25 6×6=36 ...
中学受験 · 2022/11/23
◯●●● この4個1セットがくり返されている 50番目までに4個のセット(白1黒3)がいくつ入るか 50÷4=12あまり2 12セット入る 12セット目の◯●●●で48個ある あまった2個は ◯●●● の前の2個で、◯● 49個目が白で50個目が黒 1セットに白は1つなので12セットで12個 それに49番目の白1個を加えて13個 黒は 50−13=37(個) (確認)...