中学受験
中学受験 · 2023/01/05
6の倍数は3の倍数で偶数のもの (6=2×3) 3の倍数は各位の数字の和が3で割り切れるもの 6の倍数は偶数でないといけないので □4□の 一の位は0、2、4、6、8の5通り 5通りのそれぞれに対し 百の位は3通りずつ ※ (1、4、7) (2、5、8) (3、6、9) のどれか 5×3=15(通り)
中学受験 · 2023/01/04
「ある数」の約数を探すには、かけ合わせて「ある数」になるペアの数字を見つける 12の約数は 1 2 3 12 6 4 30の約数は 1 2 3 5 30 15 10 6 2つ1組のペアだから 約数の個数は偶数であることが普通 奇数になるのはどういう場合か? 25の約数 1 5 25 5 36の約数 1 2 3 4 6 ...
中学受験 · 2022/12/25
7、14、21、28、35、42… これらは7ずつ増えていく7の倍数 7ずつ大きくなるので どのふたつを選んでも その差は7の倍数 例えば7と28の差は21 14と42の差は28 21、28、どちらも7の倍数
中学受験 · 2022/12/24
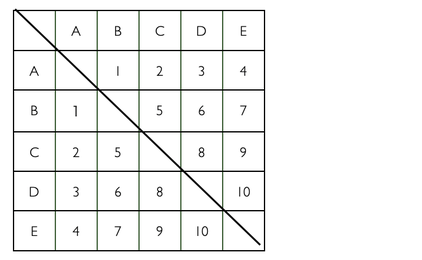
表現の仕方は違うが 「5人の中から、2人のペアを作ります。何通りできるでしょう。」 と同じ問題 5チーム(A,B,C,D,E)から2チームを選んで 順番に並べる方法は 5×4=20(通り) この中にはA,B,B,Aのように 順番が入れ替わったものがふくまれるが これは試合の組み合わせでは同じ だから2で割れば試合数がわかる 20÷2=10(通り)